Go faster Python
Preamble
This blog post gives an introduction to some techniques for benchmarking, profiling and optimising Python code. If you would like to try the code examples for yourself, you can download the Jupyter notebook (right click the “Raw” button, save link as…) that this blog post was generated from. To run the notebook, you will need a working Python 3 installation, and will also need to install a couple of Python packages. The way I did that was to first download and install miniconda into my home directory. I then ran the following from the command line:
user@host:~$ export PATH=~/miniconda3/bin/:$PATH user@host:~$ conda create -n go_faster_python python=3.5 user@host:~$ source activate go_faster_python (go_faster_python) user@host:~$ conda config --add channels conda-forge (go_faster_python) user@host:~$ conda install cython numpy jupyter line_profiler (go_faster_python) user@host:~$ jupyter notebook &
Introduction
I use Python both for writing software libraries and for interactive data analysis. Python is an interpreted, dynamically-typed language, with lots of convenient high-level data structures like lists, sets, dicts, etc. It’s great for getting things done, because no compile step means no delays when developing and testing code or when exploring data. No type declarations means lots of flexibility and less typing (on the keyboard I mean - sorry, bad joke). The high-level data structures mean you can focus on solving the problem rather than low-level nuts and bolts.
But the down-side is that Python can be slow. If you have a Python program that’s running slowly, what are your options?
Benchmarking and profiling
My intuitions for why a piece of code is running slowly are very often wrong, and many other programmers more experienced than me say the same thing. If you’re going to try and optimise something, you need to do some benchmarking and profiling first, to find out (1) exactly how slow it goes, and (2) where the bottleneck is.
To introduce some basic Python benchmarking and profiling tools, let’s look at a toy example: computing the sum of 2-dimensional array of integers. Here’s some example data:
data = [[90, 62, 33, 78, 82],
[37, 31, 0, 72, 32],
[7, 71, 79, 81, 100],
[33, 50, 66, 81, 71],
[87, 26, 54, 78, 81],
[37, 22, 96, 79, 41],
[88, 75, 100, 19, 88],
[24, 72, 59, 33, 92],
[71, 6, 59, 8, 11],
[89, 76, 65, 12, 13]]Strictly speaking this isn’t an array, it’s a list of lists. But using lists is a common and natural way to store data in Python.
Here is a naive implementation of a function called sum2d to compute the overall sum of a 2-dimensional data structure:
def sum1d(l):
"""Compute the sum of a list of numbers."""
s = 0
for x in l:
s += x
return s
def sum2d(ll):
"""Compute the sum of a list of lists of numbers."""
s = 0
for l in ll:
s += sum1d(l)
return sRun the implementation to check it works:
sum2d(data)2817
We need a bigger dataset to illustrate slow performance. To make a bigger test dataset I’m going to make use of the multiplication operator (‘*’) which when applied to a Python list will create a new list by repeating the elements of the original list. E.g., here’s the original list repeated twice:
data * 2[[90, 62, 33, 78, 82],
[37, 31, 0, 72, 32],
[7, 71, 79, 81, 100],
[33, 50, 66, 81, 71],
[87, 26, 54, 78, 81],
[37, 22, 96, 79, 41],
[88, 75, 100, 19, 88],
[24, 72, 59, 33, 92],
[71, 6, 59, 8, 11],
[89, 76, 65, 12, 13],
[90, 62, 33, 78, 82],
[37, 31, 0, 72, 32],
[7, 71, 79, 81, 100],
[33, 50, 66, 81, 71],
[87, 26, 54, 78, 81],
[37, 22, 96, 79, 41],
[88, 75, 100, 19, 88],
[24, 72, 59, 33, 92],
[71, 6, 59, 8, 11],
[89, 76, 65, 12, 13]]
Make a bigger dataset by repeating the original data a million times:
big_data = data * 1000000Now we have a dataset that is 10,000,000 rows by 5 columns:
len(big_data)10000000
len(big_data[0])5
Try running the function on these data:
sum2d(big_data)2817000000
On my laptop this takes a few seconds to run.
Benchmarking: %time, %timeit, timeit
Before you start optimising, you need a good estimate of performance as a place to start from, so you know when you’ve improved something. If you’re working in a Jupyter notebook there are a couple of magic commands available which are very helpful for benchmarking: %time and %timeit. If you’re writing a Python script to do the benchmarking, you can use the timeit module from the Python standard library.
Let’s look at the output from %time:
%time sum2d(big_data)CPU times: user 2.89 s, sys: 0 ns, total: 2.89 s
Wall time: 2.89 s
2817000000
The first line of the output gives the amount of CPU time, broken down into ‘user’ (your code) and ‘sys’ (operating system code). The second line gives the wall time, which is the actual amount of time elapsed. Generally the total CPU time and the wall time will be the same, but sometimes not. E.g., if you are benchmarking a multi-threaded program, then wall time may be less than CPU time, because CPU time counts time spent by each CPU separately and adds them together, but the CPUs may actually be working in parallel.
One thing to watch out for when benchmarking is that performance can be variable, and may be affected by other processes running on your computer. To see this happen, try running the cell above again, but while it’s running, give your computer something else to do at the same time, e.g., play some music, or a video, or just scroll the page up and down a bit.
To control for this variation, it’s a good idea to benchmark several runs (and avoid the temptation to check your email while it’s running). The %timeit magic will automatically benchmark a piece of code several times:
%timeit sum2d(big_data)1 loop, best of 3: 2.84 s per loop
Alternatively, using the timeit module:
import timeit
timeit.repeat(stmt='sum2d(big_data)', repeat=3, number=1, globals=globals())[2.892044251999323, 2.8372464299973217, 2.8505056829999376]
Function profiling: %prun, cProfile
The next thing to do is investigate which part of the code is taking the most time. If you’re working in a Jupyter notebook, the %prun command is a very convenient way to profile some code. Use it like this:
%prun sum2d(big_data)The output from %prun pops up in a separate panel, but for this blog post I need to get the output inline, so I’m going to use the cProfile module from the Python standard library directly, which does the same thing:
import cProfile
cProfile.run('sum2d(big_data)', sort='time') 10000004 function calls in 3.883 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
10000000 2.378 0.000 2.378 0.000 <ipython-input-2-12b138a62a96>:1(sum1d)
1 1.505 1.505 3.883 3.883 <ipython-input-2-12b138a62a96>:9(sum2d)
1 0.000 0.000 3.883 3.883 {built-in method builtins.exec}
1 0.000 0.000 3.883 3.883 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
There are a couple of things to notice here.
First, the time taken to execute the profiling run is quite a bit longer than the time we got when benchmarking earlier. This is because profiling adds some overhead. Generally this doesn’t affect the conclusions you would draw about which functions take the most time, but it’s something to be aware of.
Second, most of the time is being taken up in the sum1d function, although a decent amount of time is also being spent within the sum2d function. You can see this from the ‘tottime’ column, which shows the total amount of time spent within a function, not including any calls made to other functions. The ‘cumtime’ column shows the total amount of time spent in a function, including any function calls.
Also, you’ll notice that there were 10,000,004 function calls. Calling a Python function has some overhead. Maybe the code would go faster if we reduced the number of function calls? Here’s a new implementation, combining everything into a single function:
def sum2d_v2(ll):
"""Compute the sum of a list of lists of numbers."""
s = 0
for l in ll:
for x in l:
s += x
return s%timeit sum2d_v2(big_data)1 loop, best of 3: 2.22 s per loop
This is a bit faster. What does the profiler tell us?
cProfile.run('sum2d_v2(big_data)', sort='time') 4 function calls in 2.223 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
1 2.223 2.223 2.223 2.223 <ipython-input-14-81d66843d00e>:1(sum2d_v2)
1 0.000 0.000 2.223 2.223 {built-in method builtins.exec}
1 0.000 0.000 2.223 2.223 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
In fact we’ve hit a dead end here, because there is only a single function to profile, and function profiling cannot tell us which lines of code within a function are taking up most time. To get further we need to do some…
Line profiling: %lprun, line_profiler
You can do line profiling with a Python module called line_profiler. This is not part of the Python standard library, so you have to install it separately, e.g., via pip or conda.
For convenience, the line_profiler module provides a %lprun magic command for use in a Jupyter notebook, which can be used as follows:
%load_ext line_profiler%lprun -f sum2d_v2 sum2d_v2(big_data)You can also do the same thing via regular Python code:
import line_profiler
l = line_profiler.LineProfiler()
l.add_function(sum2d_v2)
l.run('sum2d_v2(big_data)')<line_profiler.LineProfiler at 0x7fcf947c4d68>
l.print_stats()Timer unit: 1e-06 s
Total time: 31.6946 s
File: <ipython-input-14-81d66843d00e>
Function: sum2d_v2 at line 1
Line # Hits Time Per Hit % Time Line Contents
==============================================================
1 def sum2d_v2(ll):
2 """Compute the sum of a list of lists of numbers."""
3 1 2 2.0 0.0 s = 0
4 10000001 2338393 0.2 7.4 for l in ll:
5 60000000 15348131 0.3 48.4 for x in l:
6 50000000 14008119 0.3 44.2 s += x
7 1 0 0.0 0.0 return s
Notice that this takes a lot longer than with just function profiling or without any profiling. Line profiling adds a lot more overhead, and this can skew benchmarking results sometimes, so it’s a good idea after each optimisation you make to benchmark without any profiling at all, as well as running function and line profiling.
If you are getting bored waiting for the line profiler to finish, you can interrupt it and it will still output some useful statistics.
Note that you have to explicitly tell line_profiler which functions to do line profiling within. When using the %lprun magic this is done via the -f option.
Most of the time is spent in the inner for loop, iterating over the inner lists, and performing the addition. Python has a built-in sum() function, maybe we could try that? …
def sum2d_v3(ll):
"""Compute the sum of a list of lists of numbers."""
s = 0
for l in ll:
x = sum(l)
s += x
return s%timeit sum2d_v3(big_data)1 loop, best of 3: 1.91 s per loop
We’ve shaved off a bit more time. What do the profiling results tell us?
cProfile.run('sum2d_v3(big_data)', sort='time') 10000004 function calls in 2.714 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
10000000 1.358 0.000 1.358 0.000 {built-in method builtins.sum}
1 1.356 1.356 2.714 2.714 <ipython-input-21-baa7cce51590>:1(sum2d_v3)
1 0.000 0.000 2.714 2.714 {built-in method builtins.exec}
1 0.000 0.000 2.714 2.714 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
import line_profiler
l = line_profiler.LineProfiler()
l.add_function(sum2d_v3)
l.run('sum2d_v3(big_data)')
l.print_stats()Timer unit: 1e-06 s
Total time: 9.65201 s
File: <ipython-input-21-baa7cce51590>
Function: sum2d_v3 at line 1
Line # Hits Time Per Hit % Time Line Contents
==============================================================
1 def sum2d_v3(ll):
2 """Compute the sum of a list of lists of numbers."""
3 1 1 1.0 0.0 s = 0
4 10000001 2536840 0.3 26.3 for l in ll:
5 10000000 4125789 0.4 42.7 x = sum(l)
6 10000000 2989380 0.3 31.0 s += x
7 1 1 1.0 0.0 return s
Now a decent amount of time is being spent inside the built-in sum() function, and there’s not much we can do about that. But there’s also still time being spent in the for loop, and in arithmetic.
You’ve probably realised by now that this is a contrived example. We’ve actually been going around in circles a bit, and our attempts at optimisation haven’t got us very far. To optimise further, we need to try something different…
NumPy
For numerical problems, the first port of call is NumPy. Let’s use it to solve the sum2d problem. First, let’s create a new test dataset, of the same size (10,000,000 rows, 5 columns), but this time using the np.random.randint() function:
import numpy as np
big_array = np.random.randint(0, 100, size=(10000000, 5))
big_arrayarray([[34, 55, 45, 16, 83],
[20, 34, 77, 55, 64],
[45, 61, 65, 8, 37],
...,
[73, 86, 73, 5, 88],
[70, 57, 92, 40, 21],
[50, 46, 93, 38, 43]])
The big_array variable is a NumPy array. Here’s a few useful properties:
# number of dimensions
big_array.ndim2
# size of each dimension
big_array.shape(10000000, 5)
# data type of each array element
big_array.dtypedtype('int64')
# number of bytes of memory used to store the data
big_array.nbytes400000000
# some other features of the array
big_array.flags C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
NumPy also has its own np.sum() function which can operate on N-dimensional arrays. Let’s try it:
%timeit np.sum(big_array)10 loops, best of 3: 30.5 ms per loop
So using NumPy is almost two orders of magnitude faster than our own Python sum2d implementation. Where does the speed come from? NumPy’s functions are implemented in C, so all of the looping and arithmetic is done in native C code. Also, a NumPy array stores it’s data in a single, contiguous block of memory, which can be accessed quickly and efficiently.
Aside: array arithmetic
There are lots of things you can do with NumPy arrays, without ever having to write a for loop. E.g.:
# column sum
np.sum(big_array, axis=0)array([494856187, 495018159, 495000327, 494824068, 494760222])
# row sum
np.sum(big_array, axis=1)array([233, 250, 216, ..., 325, 280, 270])
# add 2 to every array element
big_array + 2array([[36, 57, 47, 18, 85],
[22, 36, 79, 57, 66],
[47, 63, 67, 10, 39],
...,
[75, 88, 75, 7, 90],
[72, 59, 94, 42, 23],
[52, 48, 95, 40, 45]])
# multiply every array element by 2
big_array * 2array([[ 68, 110, 90, 32, 166],
[ 40, 68, 154, 110, 128],
[ 90, 122, 130, 16, 74],
...,
[146, 172, 146, 10, 176],
[140, 114, 184, 80, 42],
[100, 92, 186, 76, 86]])
# add two arrays element-by-element
big_array + big_arrayarray([[ 68, 110, 90, 32, 166],
[ 40, 68, 154, 110, 128],
[ 90, 122, 130, 16, 74],
...,
[146, 172, 146, 10, 176],
[140, 114, 184, 80, 42],
[100, 92, 186, 76, 86]])
# more complicated operations
t = (big_array * 2) == (big_array + big_array)
tarray([[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True],
...,
[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True]], dtype=bool)
np.all(t)True
Cython
For some problems, there is no convenient way to solve them with NumPy alone. Or in some cases, the problem can be solved with NumPy, but the solution requires too much memory. If this is the case, another option is to try optimising with Cython. Cython takes your Python code and transforms it into C code, which can then be compiled just like any other C code. A key feature is that Cython allows you to add static type declarations to certain variables, which then enables it to generate highly efficient native C code for certain critical sections of your code.
To illustrate the use of Cython I’m going to walk through an example from the Cython profiling tutorial. The task is to compute an approximate value for pi, using the formula below:
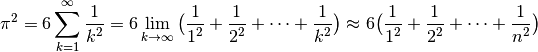
In fact there is a way to solve this problem using NumPy:
def approx_pi_numpy(n):
pi = (6 * np.sum(1 / (np.arange(1, n+1)**2)))**.5
return piapprox_pi_numpy(10000000)3.1415925580968325
%timeit approx_pi_numpy(10000000)10 loops, best of 3: 84.6 ms per loop
The NumPy solution is pretty quick, but it does require creating several reasonably large arrays in memory. If we wanted a higher precision estimate, we might run out of memory. Also, allocating memory has some overhead, and so we should be able to find a Cython solution that is even faster.
Let’s start from a pure Python solution:
def recip_square(i):
x = i**2
s = 1 / x
return s
def approx_pi(n):
"""Compute an approximate value of pi."""
val = 0
for k in range(1, n+1):
x = recip_square(k)
val += x
pi = (6 * val)**.5
return piapprox_pi(10000000)3.1415925580959025
Benchmark and profile:
%timeit approx_pi(10000000)1 loop, best of 3: 3.79 s per loop
cProfile.run('approx_pi(10000000)', sort='time') 10000004 function calls in 4.660 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
10000000 3.092 0.000 3.092 0.000 <ipython-input-42-2f54265e4169>:1(recip_square)
1 1.568 1.568 4.660 4.660 <ipython-input-42-2f54265e4169>:7(approx_pi)
1 0.000 0.000 4.660 4.660 {built-in method builtins.exec}
1 0.000 0.000 4.660 4.660 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
l = line_profiler.LineProfiler()
# l.add_function(recip_square)
l.add_function(approx_pi)
# use a smaller value of n, otherwise line profiling takes ages
l.run('approx_pi(2000000)')
l.print_stats()Timer unit: 1e-06 s
Total time: 3.36972 s
File: <ipython-input-42-2f54265e4169>
Function: approx_pi at line 7
Line # Hits Time Per Hit % Time Line Contents
==============================================================
7 def approx_pi(n):
8 """Compute an approximate value of pi."""
9 1 2 2.0 0.0 val = 0
10 2000001 676782 0.3 20.1 for k in range(1, n+1):
11 2000000 2007925 1.0 59.6 x = recip_square(k)
12 2000000 685011 0.3 20.3 val += x
13 1 5 5.0 0.0 pi = (6 * val)**.5
14 1 0 0.0 0.0 return pi
Notice that I commented out line profiling for the recip_square() function. If you’re running this yourself, I recommend running line profiling with and without including recip_square(), and each time take a look at the results for the outer approx_pi() function. This is a good example of how the overhead of line profiling can skew timings, so again, something to beware of.
Now let’s start constructing a Cython implementation. If you’re working in a Jupyter notebook, there is a very convenient %%cython magic which enables you to write a Cython module within the notebook. When you execute a %%cython code cell, behind the scenes Cython will generate and compile your module, and import the functions into the current session so they can be called from other code cells. To make the %%cython magic available, we need to load the Cython notebook extension:
%load_ext cythonTo begin with, all I’ll do is copy-paste the pure Python implementation into the Cython module, then change the function names so we can benchmark and profile separately:
%%cython
def recip_square_cy1(i):
x = i**2
s = 1 / x
return s
def approx_pi_cy1(n):
"""Compute an approximate value of pi."""
val = 0
for k in range(1, n+1):
x = recip_square_cy1(k)
val += x
pi = (6 * val)**.5
return piapprox_pi_cy1(10000000)3.1415925580959025
%timeit approx_pi_cy1(10000000)1 loop, best of 3: 2.74 s per loop
Notice that the Cython function is a bit faster than the pure-Python function, even though the code is identical. However, we’re still a long way short of the NumPy implementation.
What we’re going to do next is make a number of modifications to the Cython implementation. If you’re working through this in a notebook, I recommend copy-pasting the Cython code cell from above into a new empty code cell below, and changing the function names to approx_py_cy2() and recip_square_cy2(). Then, work through the optimisation steps below, one-by-one. After each step, run benchmarking and profiling to see where and how much speed has been gained, and examine the HTML diagnostics generated by Cython to see how much yellow (Python interaction) there is left. The goal is to remove all yellow from critical sections of the code.
- Copy-paste Cython code cell from above into a new cell below; rename
approx_pi_cy1toapprox_pi_cy2andrecip_square_cy1torecip_square_cy2. Be careful to rename all occurrences of the function names. - Change
%%cythonto%%cython -aat the top of the cell. Adding the-aflag causes Cython to generate an HTML document with some diagnostics. This includes colouring of every line of code according to how much interaction is happening with Python. The more you can remove interaction with Python, the more Cython can optimise and generate efficient native C code. - Add support for function profiling by adding the following comment (special comments like this are interpreted by Cython as compiler directives):
# cython: profile=True
- Add support for line profiling by adding the following comments:
# cython: linetrace=True # cython: binding=True # distutils: define_macros=CYTHON_TRACE_NOGIL=1
The following steps optimise the recip_square function:
- Add a static type declaration for the
iargument to therecip_squarefunction, by changing the function signature fromrecip_square(i)torecip_square(int i). - Add static type declarations for the
xandsvariables within therecip_squarefunction, via acdefsection at the start of the function. - Tell Cython to use C division instead of Python division within the
recip_squarefunction by adding the@cython.cdivision(True)annotation immediately above the function definition. This also requires adding the import statementcimport cython.
Now the recip_square function should be fully optimised. The following steps optimise the outer approx_pi_cy2 function:
- Optimise the
forloop by adding static type declarations for thenargument and thekvariable. - Make
recip_squareacdeffunction and add a return type. - Add a static type declaration for the
valvariable. - Remove line profiling support.
- Remove function profiling support.
- Make
recip_squareaninlinefunction.
Here is the end result…
%%cython -a
cimport cython
@cython.cdivision(True)
cdef inline double recip_square_cy2(int i):
cdef:
double x, s
x = i**2
s = 1 / x
return s
def approx_pi_cy2(int n):
"""Compute an approximate value of pi."""
cdef:
int k
double val
val = 0
for k in range(1, n+1):
x = recip_square_cy2(k)
val += x
pi = (6 * val)**.5
return piGenerated by Cython 0.25.2
Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.
01:
02:
03: cimport cython
04:
05:
06: @cython.cdivision(True)
+07: cdef inline double recip_square_cy2(int i):
static CYTHON_INLINE double __pyx_f_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_recip_square_cy2(int __pyx_v_i) {
double __pyx_v_x;
double __pyx_v_s;
double __pyx_r;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("recip_square_cy2", 0);
/* … */
/* function exit code */
__pyx_L0:;
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
08: cdef:
09: double x, s
+10: x = i**2
__pyx_v_x = __Pyx_pow_long(((long)__pyx_v_i), 2);
+11: s = 1 / x
__pyx_v_s = (1.0 / __pyx_v_x);
+12: return s
__pyx_r = __pyx_v_s; goto __pyx_L0;
13:
14:
+15: def approx_pi_cy2(int n):
/* Python wrapper */
static PyObject *__pyx_pw_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_1approx_pi_cy2(PyObject *__pyx_self, PyObject *__pyx_arg_n); /*proto*/
static char __pyx_doc_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_approx_pi_cy2[] = "Compute an approximate value of pi.";
static PyMethodDef __pyx_mdef_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_1approx_pi_cy2 = {"approx_pi_cy2", (PyCFunction)__pyx_pw_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_1approx_pi_cy2, METH_O, __pyx_doc_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_approx_pi_cy2};
static PyObject *__pyx_pw_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_1approx_pi_cy2(PyObject *__pyx_self, PyObject *__pyx_arg_n) {
int __pyx_v_n;
PyObject *__pyx_r = 0;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("approx_pi_cy2 (wrapper)", 0);
assert(__pyx_arg_n); {
__pyx_v_n = __Pyx_PyInt_As_int(__pyx_arg_n); if (unlikely((__pyx_v_n == (int)-1) && PyErr_Occurred())) __PYX_ERR(0, 15, __pyx_L3_error)
}
goto __pyx_L4_argument_unpacking_done;
__pyx_L3_error:;
__Pyx_AddTraceback("_cython_magic_c1207dcff1d0d009517ab1cb3466abf5.approx_pi_cy2", __pyx_clineno, __pyx_lineno, __pyx_filename);
__Pyx_RefNannyFinishContext();
return NULL;
__pyx_L4_argument_unpacking_done:;
__pyx_r = __pyx_pf_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_approx_pi_cy2(__pyx_self, ((int)__pyx_v_n));
/* function exit code */
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
static PyObject *__pyx_pf_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_approx_pi_cy2(CYTHON_UNUSED PyObject *__pyx_self, int __pyx_v_n) {
int __pyx_v_k;
double __pyx_v_val;
double __pyx_v_x;
double __pyx_v_pi;
PyObject *__pyx_r = NULL;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("approx_pi_cy2", 0);
/* … */
/* function exit code */
__pyx_L1_error:;
__Pyx_XDECREF(__pyx_t_3);
__Pyx_AddTraceback("_cython_magic_c1207dcff1d0d009517ab1cb3466abf5.approx_pi_cy2", __pyx_clineno, __pyx_lineno, __pyx_filename);
__pyx_r = NULL;
__pyx_L0:;
__Pyx_XGIVEREF(__pyx_r);
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
/* … */
__pyx_tuple_ = PyTuple_Pack(6, __pyx_n_s_n, __pyx_n_s_n, __pyx_n_s_k, __pyx_n_s_val, __pyx_n_s_x, __pyx_n_s_pi); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 15, __pyx_L1_error)
__Pyx_GOTREF(__pyx_tuple_);
__Pyx_GIVEREF(__pyx_tuple_);
/* … */
__pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_1approx_pi_cy2, NULL, __pyx_n_s_cython_magic_c1207dcff1d0d00951); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 15, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_1);
if (PyDict_SetItem(__pyx_d, __pyx_n_s_approx_pi_cy2, __pyx_t_1) < 0) __PYX_ERR(0, 15, __pyx_L1_error)
__Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
16: """Compute an approximate value of pi."""
17: cdef:
18: int k
19: double val
+20: val = 0
__pyx_v_val = 0.0;
+21: for k in range(1, n+1):
__pyx_t_1 = (__pyx_v_n + 1);
for (__pyx_t_2 = 1; __pyx_t_2 < __pyx_t_1; __pyx_t_2+=1) {
__pyx_v_k = __pyx_t_2;
+22: x = recip_square_cy2(k)
__pyx_v_x = __pyx_f_46_cython_magic_c1207dcff1d0d009517ab1cb3466abf5_recip_square_cy2(__pyx_v_k);
+23: val += x
__pyx_v_val = (__pyx_v_val + __pyx_v_x); }
+24: pi = (6 * val)**.5
__pyx_v_pi = pow((6.0 * __pyx_v_val), .5);
+25: return pi
__Pyx_XDECREF(__pyx_r); __pyx_t_3 = PyFloat_FromDouble(__pyx_v_pi); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 25, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_3); __pyx_r = __pyx_t_3; __pyx_t_3 = 0; goto __pyx_L0;
%timeit approx_pi_cy2(10000000)100 loops, best of 3: 11.6 ms per loop
cProfile.run('approx_pi_cy2(10000000)', sort='time')l = line_profiler.LineProfiler()
# l.add_function(recip_square_cy2)
l.add_function(approx_pi_cy2)
# use a smaller value of n, otherwise line profiling takes ages
l.run('approx_pi_cy2(2000000)')
l.print_stats()So the optimised Cython implementation is about 8 times faster than the NumPy implementation. You may have noticed that a couple of the optimisation steps didn’t actually make much difference to performance, and so weren’t really necessary.
Cython and NumPy
Finally, here’s a Cython implementation of the sum2d function, just to give an example of how to use Cython and NumPy together. As above, you may want to introduce the optimisations one at a time, and benchmark and profile after each step, to get a sense of which optimisations really make a difference.
%%cython -a
cimport numpy as np
cimport cython
@cython.wraparound(False)
@cython.boundscheck(False)
def sum2d_cy(np.int64_t[:, :] ll):
"""Compute the sum of a 2-dimensional array of integers."""
cdef:
int i, j
np.int64_t s
s = 0
for i in range(ll.shape[0]):
for j in range(ll.shape[1]):
s += ll[i, j]
return sGenerated by Cython 0.25.2
Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.
01:
02:
+03: cimport numpy as np
__pyx_t_1 = PyDict_New(); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 3, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_1); if (PyDict_SetItem(__pyx_d, __pyx_n_s_test, __pyx_t_1) < 0) __PYX_ERR(0, 3, __pyx_L1_error) __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
04: cimport cython
05:
06:
07: @cython.wraparound(False)
08: @cython.boundscheck(False)
+09: def sum2d_cy(np.int64_t[:, :] ll):
/* Python wrapper */
static PyObject *__pyx_pw_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_1sum2d_cy(PyObject *__pyx_self, PyObject *__pyx_arg_ll); /*proto*/
static char __pyx_doc_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_sum2d_cy[] = "Compute the sum of a 2-dimensional array of integers.";
static PyMethodDef __pyx_mdef_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_1sum2d_cy = {"sum2d_cy", (PyCFunction)__pyx_pw_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_1sum2d_cy, METH_O, __pyx_doc_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_sum2d_cy};
static PyObject *__pyx_pw_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_1sum2d_cy(PyObject *__pyx_self, PyObject *__pyx_arg_ll) {
__Pyx_memviewslice __pyx_v_ll = { 0, 0, { 0 }, { 0 }, { 0 } };
PyObject *__pyx_r = 0;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("sum2d_cy (wrapper)", 0);
assert(__pyx_arg_ll); {
__pyx_v_ll = __Pyx_PyObject_to_MemoryviewSlice_dsds_nn___pyx_t_5numpy_int64_t(__pyx_arg_ll); if (unlikely(!__pyx_v_ll.memview)) __PYX_ERR(0, 9, __pyx_L3_error)
}
goto __pyx_L4_argument_unpacking_done;
__pyx_L3_error:;
__Pyx_AddTraceback("_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24.sum2d_cy", __pyx_clineno, __pyx_lineno, __pyx_filename);
__Pyx_RefNannyFinishContext();
return NULL;
__pyx_L4_argument_unpacking_done:;
__pyx_r = __pyx_pf_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_sum2d_cy(__pyx_self, __pyx_v_ll);
/* function exit code */
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
static PyObject *__pyx_pf_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_sum2d_cy(CYTHON_UNUSED PyObject *__pyx_self, __Pyx_memviewslice __pyx_v_ll) {
int __pyx_v_i;
int __pyx_v_j;
__pyx_t_5numpy_int64_t __pyx_v_s;
PyObject *__pyx_r = NULL;
__Pyx_RefNannyDeclarations
__Pyx_RefNannySetupContext("sum2d_cy", 0);
/* … */
/* function exit code */
__pyx_L1_error:;
__Pyx_XDECREF(__pyx_t_7);
__Pyx_AddTraceback("_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24.sum2d_cy", __pyx_clineno, __pyx_lineno, __pyx_filename);
__pyx_r = NULL;
__pyx_L0:;
__PYX_XDEC_MEMVIEW(&__pyx_v_ll, 1);
__Pyx_XGIVEREF(__pyx_r);
__Pyx_RefNannyFinishContext();
return __pyx_r;
}
/* … */
__pyx_tuple__23 = PyTuple_Pack(5, __pyx_n_s_ll, __pyx_n_s_ll, __pyx_n_s_i, __pyx_n_s_j, __pyx_n_s_s); if (unlikely(!__pyx_tuple__23)) __PYX_ERR(0, 9, __pyx_L1_error)
__Pyx_GOTREF(__pyx_tuple__23);
__Pyx_GIVEREF(__pyx_tuple__23);
/* … */
__pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_46_cython_magic_e638c34ce8e90ea82c9e0687d99dcc24_1sum2d_cy, NULL, __pyx_n_s_cython_magic_e638c34ce8e90ea82c); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 9, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_1);
if (PyDict_SetItem(__pyx_d, __pyx_n_s_sum2d_cy, __pyx_t_1) < 0) __PYX_ERR(0, 9, __pyx_L1_error)
__Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
__pyx_codeobj__24 = (PyObject*)__Pyx_PyCode_New(1, 0, 5, 0, 0, __pyx_empty_bytes, __pyx_empty_tuple, __pyx_empty_tuple, __pyx_tuple__23, __pyx_empty_tuple, __pyx_empty_tuple, __pyx_kp_s_home_aliman_cache_ipython_cytho, __pyx_n_s_sum2d_cy, 9, __pyx_empty_bytes); if (unlikely(!__pyx_codeobj__24)) __PYX_ERR(0, 9, __pyx_L1_error)
10: """Compute the sum of a 2-dimensional array of integers."""
11: cdef:
12: int i, j
13: np.int64_t s
+14: s = 0
__pyx_v_s = 0;
+15: for i in range(ll.shape[0]):
__pyx_t_1 = (__pyx_v_ll.shape[0]);
for (__pyx_t_2 = 0; __pyx_t_2 < __pyx_t_1; __pyx_t_2+=1) {
__pyx_v_i = __pyx_t_2;
+16: for j in range(ll.shape[1]):
__pyx_t_3 = (__pyx_v_ll.shape[1]);
for (__pyx_t_4 = 0; __pyx_t_4 < __pyx_t_3; __pyx_t_4+=1) {
__pyx_v_j = __pyx_t_4;
+17: s += ll[i, j]
__pyx_t_5 = __pyx_v_i;
__pyx_t_6 = __pyx_v_j;
__pyx_v_s = (__pyx_v_s + (*((__pyx_t_5numpy_int64_t *) ( /* dim=1 */ (( /* dim=0 */ (__pyx_v_ll.data + __pyx_t_5 * __pyx_v_ll.strides[0]) ) + __pyx_t_6 * __pyx_v_ll.strides[1]) ))));
}
}
+18: return s
__Pyx_XDECREF(__pyx_r); __pyx_t_7 = __Pyx_PyInt_From_npy_int64(__pyx_v_s); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 18, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_7); __pyx_r = __pyx_t_7; __pyx_t_7 = 0; goto __pyx_L0;
%timeit sum2d_cy(big_array)10 loops, best of 3: 34.3 ms per loop
%timeit np.sum(big_array)10 loops, best of 3: 30.4 ms per loop
In this case the Cython and NumPy implementations are nearly identical, so there is no value in using Cython.
Further reading
There are loads of good resources on the Web on the topics covered here. Here’s just a few:
- The Python profilers
- A guide to analyzing Python performance by Huy Nguyen
- SnakeViz
- NumPy tutorial
- Cython tutorials
- The fallacy of premature optimization by Randall Hyde